Товары по запросу: "что такое гипербола в математике"
В категории "Крючки и ручки" такого товара не найдено
Чаще всего в данной категории ищут:
- путин ручка кнопка
- ручки кнопки бронза латунь
- ручки для входных дверей латунь скоба
- крючок для вешалки однорожковый
- ручка скоба рс 100 белый
- дверные ручки скобы для входных
- ручка скоба 8 1115
- ручка кнопка сердечко
- ручка дверная скоба под старину
- ручка кпп с кнопкой купить
- ручки капля для шкафа
- ручка скоба 305128mp02
- купить ручку скобу для стеклянной двери
- пластиковая заглушка для винта
- кнопка ручке двери
- дверные ручки скобы для входных дверей
- ручка скоба brass золото
- ручки скоба античные
- мебельные ручки скоба бронза купить
- ручка кнопка к5
Фотоальбом:
Гипербола в Математике [уравнение + 10 примеров]
Презентация "Что такое гипербола?" по математике

математическая гипербола. Как построить гиперболу?

Гипербола в математике. формула, примеры, уравнение

Гипербола в математике. формула, примеры, уравнение

Гипербола Фото Математика

Презентация "Что такое гипербола?" по математике
Гипербола Фото Математика

Комментарии:
Гипербола (математика)
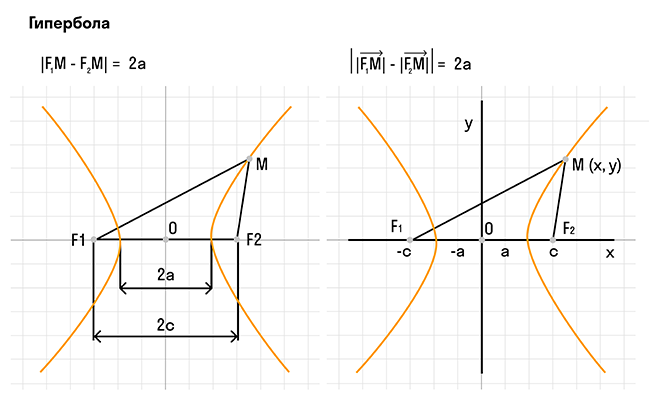
Гипе́рбола (др.-греч. ὑπερβολή, от ὑπερ — «верх» + βαλειν — «бросать») — геометрическое место точек M евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек и (называемых фокусами) постоянно. Точнее, > {\displaystyle |F_ {1}F_ {2}|>2a>0.}
Гипербола в Математике [уравнение + 10 примеров]
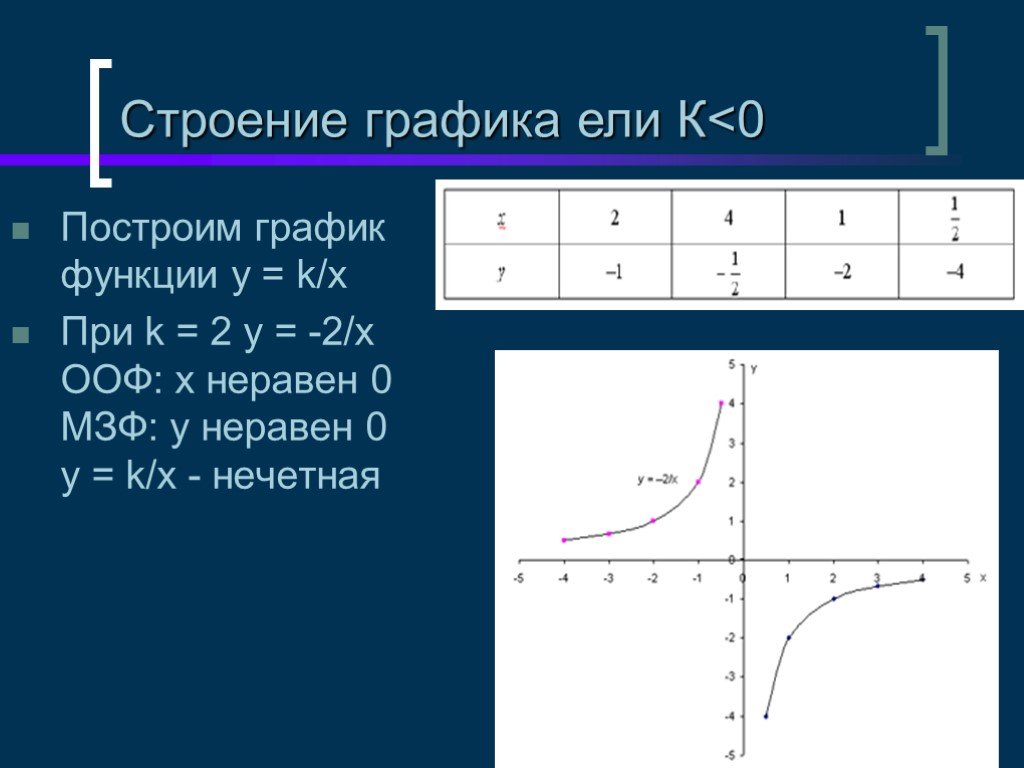
Гипербола — это кривая, определяемая формулой (каноническая форма). У гиперболы есть две ветви, которые разбегаются. Примеры: если (k < 0) — в II и IV. Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Что такое гипербола в математике: основные понятия и свойства
В этой статье мы подробно разбираем, что такое гипербола в математике. Рассматриваются геометрическое определение гиперболы, ее аналитическое задание, основные свойства и характеристики.
Что такое гипербола в математике?
Гипербола — одна из важнейших кривых в аналитической геометрии, имеющая широкое применение в различных науках, технике и даже искусстве. Эта статья рассмотрит основные свойства гиперболы, её определение и способы использования в разных дисциплинах.
Что такое гипербола: определение, функция, формула, примеры построения
Гипербола - это график функции обратной пропорциональности, которая в общем виде задается следующей формулой: Здесь: x - независимая переменная; k ≠ 0;
Гипербола и парабола
Начнём с общего понятия гиперболы и задачи на её построение. Каноническое уравнение гиперболы имеет вид , где - положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие , то есть значение «а» может быть и меньше значения «бэ».
Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и есть величина постоянная , меньшая расстояния между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Что такое гипербола: уравнения и свойства
В этой статье рассказывается о том, что такое гипербола, приведена формула гиперболы, а также рассмотрены свойства её свойства и основные определения.
Что такое гипербола
Гипербола - это геометрическая фигура, которая представляет собой множество точек на плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек, называемых фокусами, постоянна. Гипербола имеет две ветви, которые расходятся от центра, который является точкой пересечения осей симметрии.
Гипербола в математике: формула и свойства гиперболы, уравнение и как
Что такое гипербола? Гипербола — это кривая второго порядка, задаваемая каноническим уравнением вида a и b — параметры, определяющие форму гиперболы.